Wisconsin State Hex Grid - Mapping 2016 Presidential Results

Use the hexmapr package to map the Wisconsin 2016 Presidential Results

NOTE: find this package here:

https://github.com/hafen/hexmapr with `devtools::install_github("hafen/hexmapr")`

NEAT PACKAGE ALERT!

I’ve been thinking about implementing something like this for a while - got excited by this tweet I thought I would do some exploring and write out a post over the weekend. Creating a county-level hex grid of Wisconsin makes for a perfect supplment to my earlier post about mapping the 2016 Wisconsin presidential results.

Let’s make a hex grid of Wisconsin

The first thing we’ll do is retrieve a Wisconsin shapefile; we can use the tigris package developed by Kyle Walker to pull a 2010 census shapefile of Wisconsin counties:

library(tigris)
wi <- counties("Wisconsin", cb = TRUE)
wi_original <- wi
plot(wi)

WI tigris shapefile

We’ll then port some code from the hexmapr github README:

devtools::install_github("sassalley/hexmapr")
library(hexmapr)
wi_details <- hexmapr::get_shape_details(wi)
wi@data$xcentroid <- coordinates(wi)[,1]
wi@data$ycentroid <- coordinates(wi)[,2]

We’re going for the closest shapefile match, preferring a final shape than looks like the outline of the state than one with appropriate placement of counties - there is rarely a perfect grid match. So let’s test a whole bunch:

# hexagon - red border for the 28th seed
png(file = "/home/michael/Documents/mikeleeco.github.com/static/img/hexGridWisconsin.png", width = 700, height = 500)
par(mfrow=c(7,5), mar = c(0,1,2,1))
for (i in 1:35){
  new_cells <-  calculate_cell_size(wi, wi_details,0.03, 'hexagonal', i)
  if(i == 28) {
    plot(new_cells[[2]], main = paste("Seed",i, sep=" "), border = "red")
  } else {
    plot(new_cells[[2]], main = paste("Seed",i, sep=" "))
  }
}

# squares - red border for the 7th seed
png(file = "/home/michael/Documents/mikeleeco.github.com/static/img/squareGridWisconsin.png", width = 700, height = 500)
par(mfrow=c(7,5), mar = c(0,1,2,1))
for (i in 1:35){
  new_cells <-  calculate_cell_size(wi, wi_details,0.03, 'regular', i)
  if(i == 7) {
    plot(new_cells[[2]], main = paste("Seed",i, sep=" "), border = "red")
  } else {
    plot(new_cells[[2]], main = paste("Seed",i, sep=" "))
  }
}

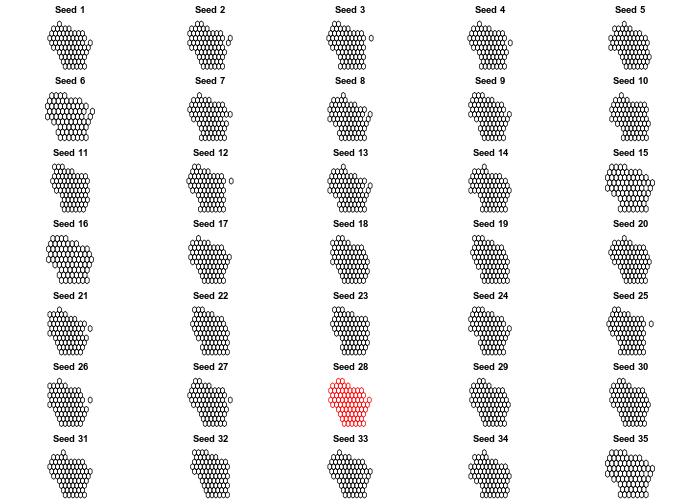
hex grid options

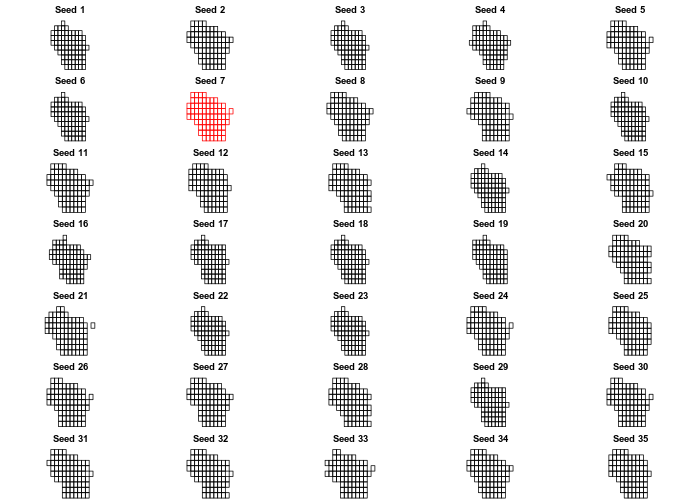
square grid options

I like the look of the 28th hexagon grid, and the 7th square grid. Let’s take those and assign the polygons to a new SpatialPolygonsDataFrame, then fortify .

library(dplyr)
library(ggplot2)
clean <- function(shape){
  shape@data$id = rownames(shape@data)
  shape.points = fortify(shape, region="id")
  shape.df = left_join(shape.points, shape@data, by="id")
}

new_cells_hex <-  calculate_cell_size(wi_original, wi_details,0.03, 'hexagonal', 28)
resulthex <- assign_polygons(wi_original,new_cells_hex)
result_df_hex <- clean(resulthex)

new_cells_square <-  calculate_cell_size(wi_original, wi_details,0.03, 'regular', 7)
resultsquare <- assign_polygons(wi_original,new_cells_square)
result_df_square <- clean(resultsquare)

Now that we’ve got our modified SpatialPolygonsDataFrames - covered to a dataframe for use with ggplot2 - we can plot the result using geom_polygon:

library(viridis)
library(extrafont)
loadfonts()
theme_open_sans <- theme(text=element_text(family="Open Sans"), plot.title = element_text(family = "Open Sans Semibold", size = 24), plot.subtitle = element_text(family = "Open Sans Light",size = 14), legend.title = element_text(family="Open Sans Semibold"))
hexplot <- ggplot(result_df_hex) +
  geom_polygon(aes(x=long, y=lat, fill = as.numeric(ALAND), group = group))+
  geom_text(aes(V1, V2, label = NAME), size=2.5, color = "white", family = "Open Sans") +
  scale_fill_viridis() +
  guides(fill=FALSE) +
  theme_void() + theme_open_sans

hexplot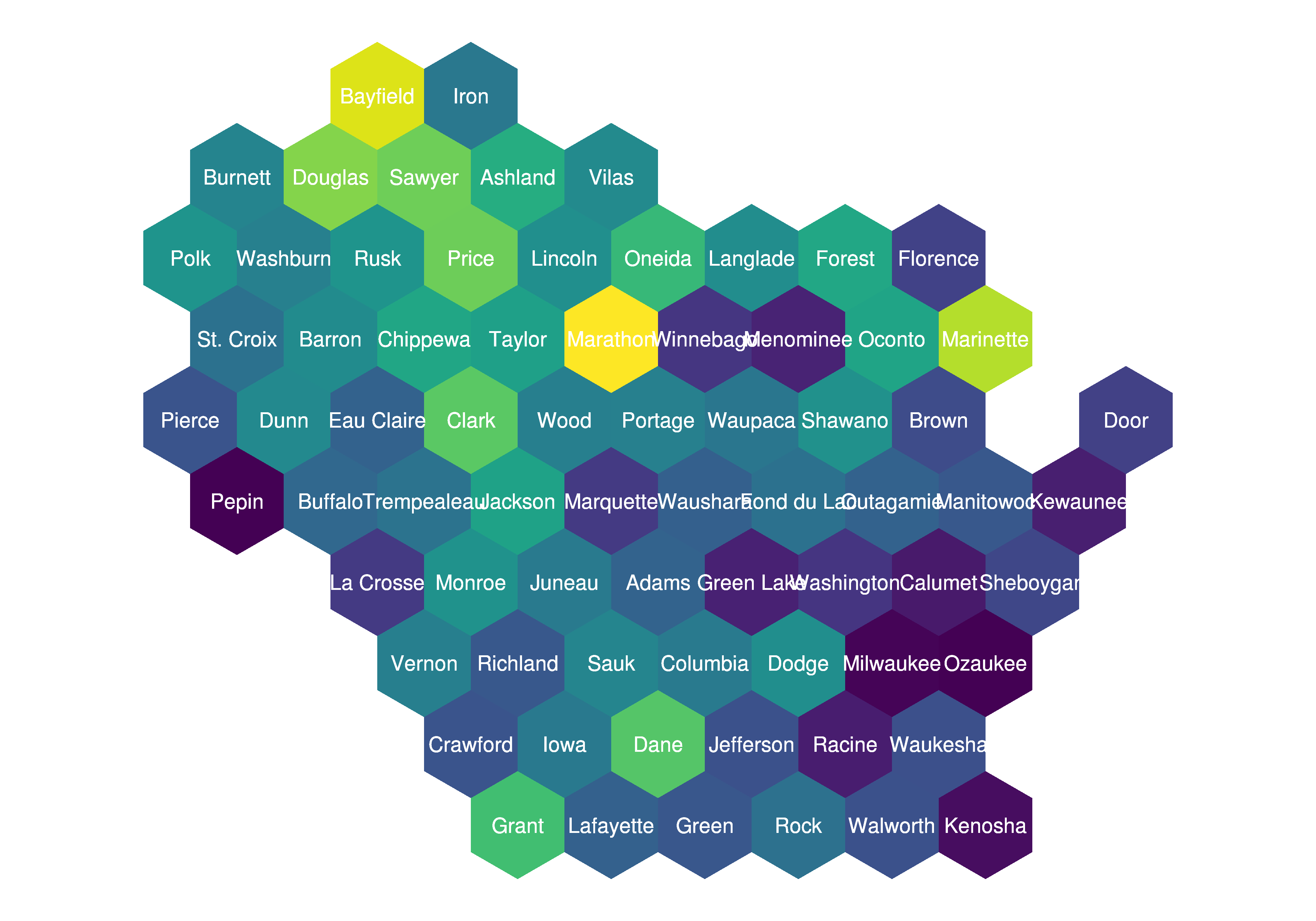

Wisconsin Hex Grid Map by County by ALAND

squareplot <- ggplot(result_df_square) +
  geom_polygon(aes(x=long, y=lat, fill = as.numeric(ALAND), group = group))+
  geom_text(aes(V1, V2, label = NAME), size=2.5, color = "white", family = "Open Sans") +
  scale_fill_viridis() +
  guides(fill=FALSE) +
  theme_void() + theme_open_sans

squareplot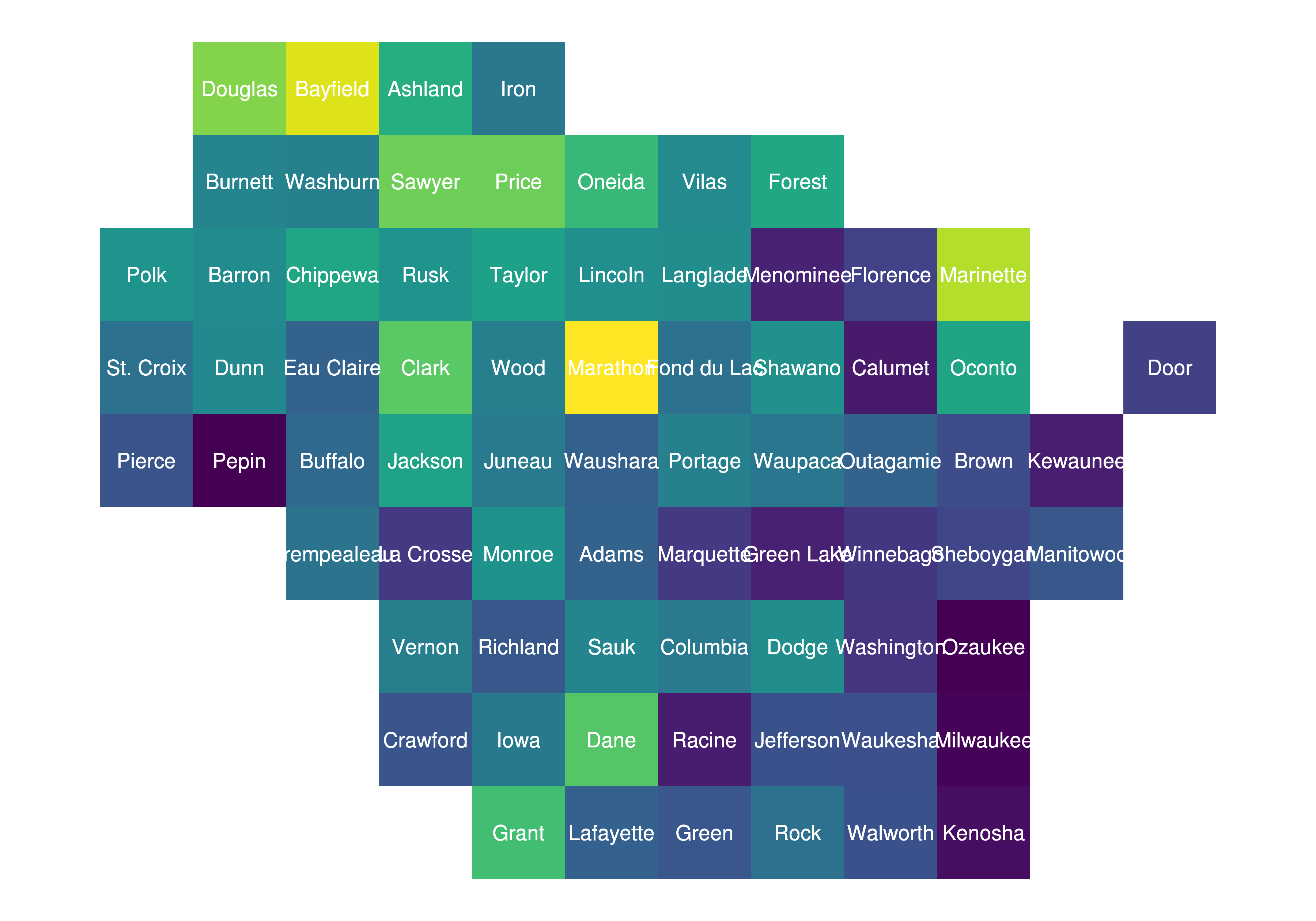

Wisconsin Square Grid Map by County by ALAND

I saw on twitter that sf can now be used natively, so I gave that I try as well. First convert the SpatialPolygonsDataFrame to a simple feature (sf), then plot the resultant object using geom_sf:

sfResultSquare <- st_as_sf(resultsquare)
sfResultHex <- st_as_sf(resulthex)
class(sfResultHex)
sfHexPlot <-ggplot(sfResultHex) +
    geom_sf(aes(fill = as.numeric(ALAND)), color = "transparent") +
    geom_text(aes(V1, V2, label = NAME), size=2.5, color = "white", family = "Open Sans") +
    scale_fill_viridis() +
    guides(fill=FALSE) +
    theme(panel.background = element_rect(fill = NA), axis.text = element_blank(), axis.ticks = element_blank(), axis.title = element_blank())

sfHexPlot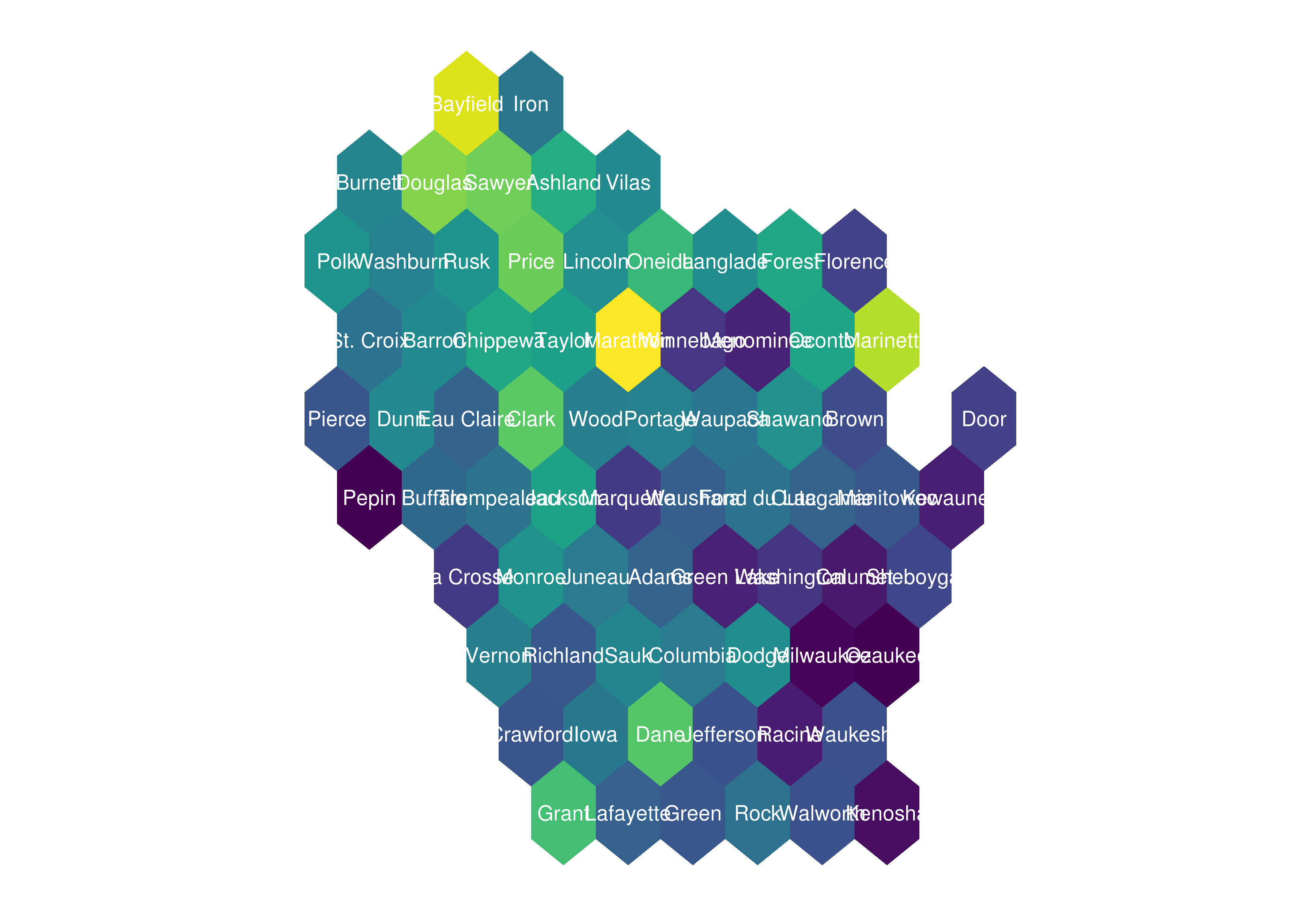

Wisconsin Square Grid Map by County by ALAND using geom_sf

Cool to know that’s possible! Let’s use some more novel data than land area. Building off of a previous post mapping Wisconsin presidential election results, let’s map vote totals to our new gridmaps.

library(stringr)
library(tidyr)
all_results <- read.csv("https://raw.githubusercontent.com/mkearney/presidential_election_county_results_2016/master/pres16results.csv", stringsAsFactors = FALSE)

wisconsin <- all_results %>%
  filter(str_detect(fips, "^55"))

wisconsin_spread <- wisconsin %>%
  filter(cand %in% c("Donald Trump", "Hillary Clinton")) %>%
  select(fips, cand, votes, total_votes) %>%
  spread(cand, votes)

wisconsin_spread <- wisconsin_spread %>% mutate(voteDiff = `Donald Trump` - `Hillary Clinton`,
                                                pctDiff = `Donald Trump`/total_votes - `Hillary Clinton`/total_votes,
                                                weight = total_votes/ sum(total_votes))
wisconsin_spread$weight <- ifelse(wisconsin_spread$pctDiff > 0 , -wisconsin_spread$weight, wisconsin_spread$weight)

We can create some custom breaks to give counties with higher vote totals more prominence in the figure, then merge these onto our hex and square SpatialPolygonsDataFrame:

wisconsin_spread$breaks <- cut(wisconsin_spread$weight,
                               breaks = c(-1, -.1, -0.05, -0.01, 0, 0.01, .05, .1, 1),
                               labels = c("R   More than 10 Percent", "R   5 to 10 Percent", "R   1 to 5 Percent", "R   Less than 1 Percent",
                                          "D   Less than 1 Percent","D   1 to 5 Percent", "D   5 to 10 Percent", "D   More than 10 Percent"))
wiHex <- merge(result_df_hex, wisconsin_spread, by.x = "GEOID", by.y = "fips")
wiSquare <- merge(result_df_square, wisconsin_spread, by.x = "GEOID", by.y = "fips")

Once we’ve got our data sets finalized, figures are created usng geom_polygon:

library(RColorBrewer)

wiHexPlot <- ggplot(wiHex) +
    geom_polygon(aes(x=long, y=lat, fill=breaks, group = group), color = "#f5f5f5") +
    geom_text(aes(V1, V2, label = NAME), size=2.5, color = "black", family = "Open Sans") +
    scale_fill_manual(name = "Portion of WI Vote", values = brewer.pal(8, "RdBu"), drop = FALSE) +
    guides(alpha=FALSE) +
    ggtitle(label = "2016 Presidential Results by Wisconsin Counties", subtitle = "59 of 72 Wisconsin counties leaned Republican, while the only two counties with\nmore than 10 percent of the state's votes totaled more Democratic votes") +
    theme(panel.background = element_rect(fill = NA), axis.text = element_blank(), axis.ticks = element_blank(), axis.title = element_blank()) +
    theme_open_sans

wiHexPlot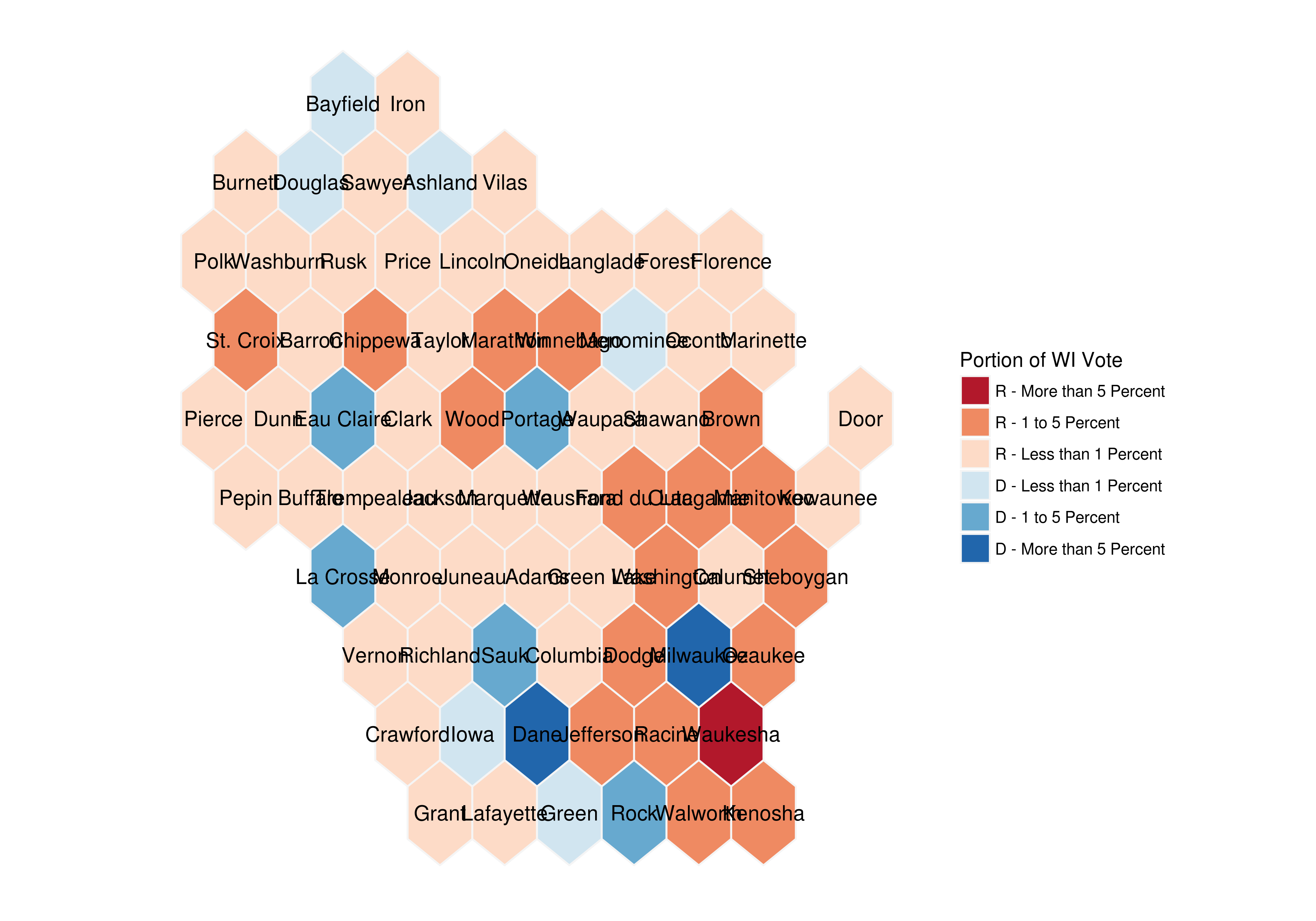

Wisconsin Hex Grid Map by County by Vote Count

wiSquarePlot <- ggplot(wiSquare) +
    geom_polygon(aes(x=long, y=lat, fill=breaks, group = group), color = "#f5f5f5") +
    geom_text(aes(V1, V2, label = NAME), size=2.5, color = "black", family = "Open Sans") +
    scale_fill_manual(name = "Percentage of WI Vote Total", values = brewer.pal(8, "RdBu"), drop = FALSE) +
    guides(alpha=FALSE) +
    ggtitle(label = "2016 Presidential Results by Wisconsin Counties", subtitle = "59 of 72 Wisconsin counties leaned Republican, while the only two counties with\nmore than 10 percent of the state's votes totaled more Democratic votes") +
    theme(panel.background = element_rect(fill = NA), axis.text = element_blank(), axis.ticks = element_blank(), axis.title = element_blank()) +
    theme_open_sans

wiSquarePlot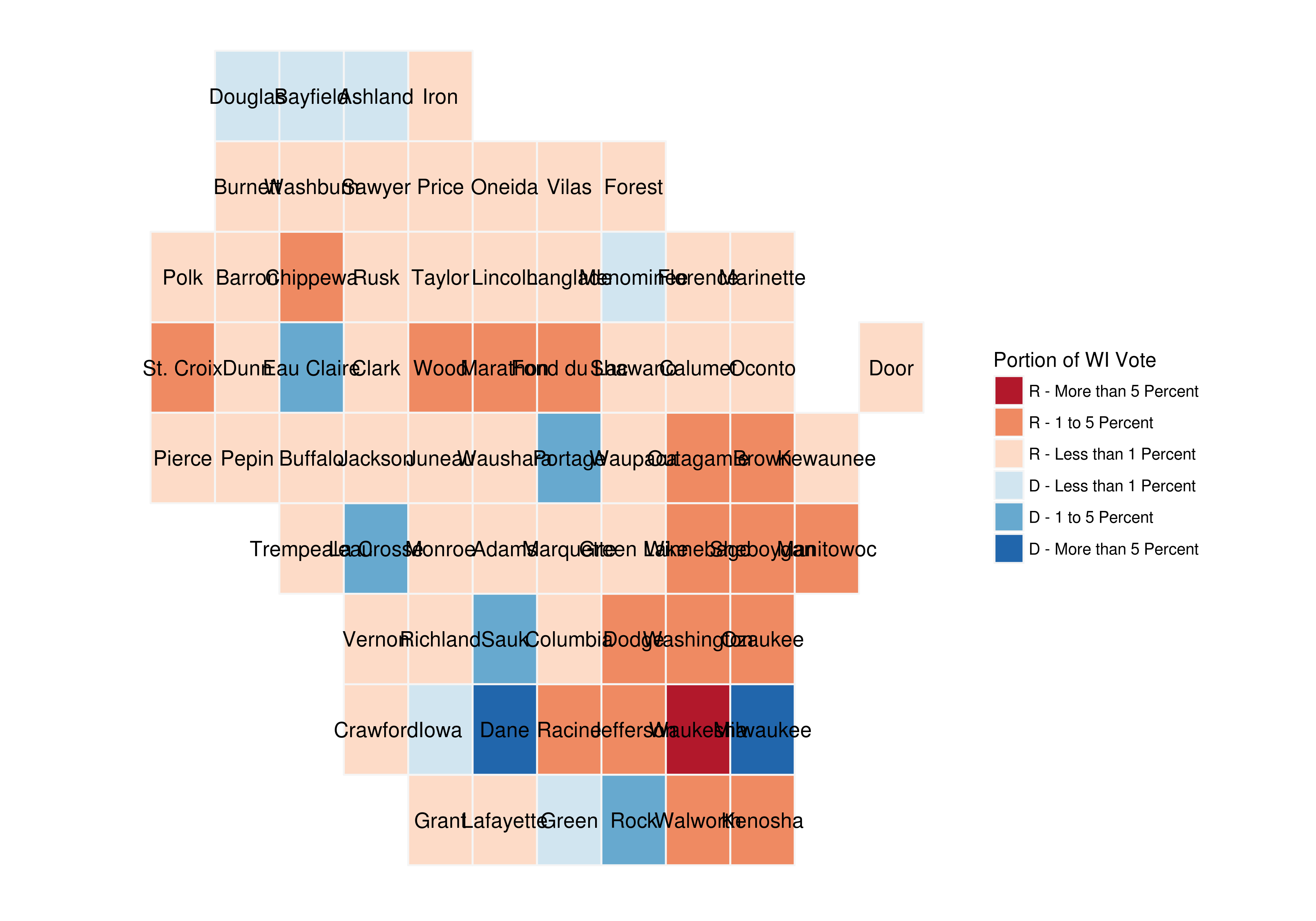

Wisconsin Square Grid Map by County by Vote Count

Interested in learning more? Hire me to consult on your next project, follow me on twitter, or contact me via email. All inquiries welcome!

← Back to all posts